

Dramatically Improve the Quality of Your Strategic Business Decisions
링크를 클릭하시면 몬테카를로 시뮬레이션을 활용한 불확실한 프로젝트 관리가 왜 필요한지 쉽게 알수 있습니다.
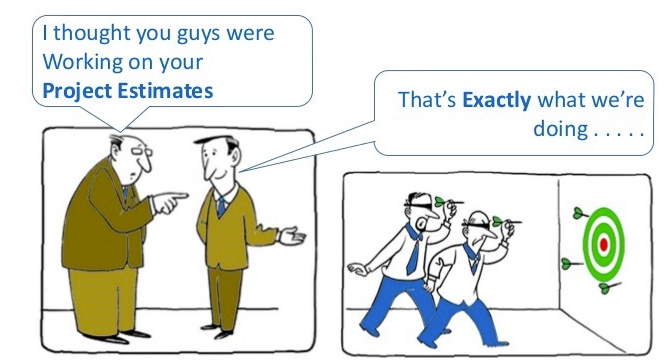
왜 확률론적 분석 방법이 필요한지를 잘 설명해 주고 있는 페이퍼인것 같다.
우리들은 리스크를 관리하기 위해서 정량적인 분석 방법들을 활용하게 된다. 우리가 직면하고 있는 비즈니스 상황이나 프로젝트들과 관련된 많은 요인들이 불확실성을 포함하고 있는 데도 불구하고 이러한 부분들은 간과하고 하나의 결과값을 추정하는 결정론적 의사결정 방법을 활용한다.
이러한 결정론적 의사결정 방법이 틀리다는 것은 아니다 하지만 이러한 방법의 한계는 실제 발생가능한 리스크를 고려하지 못한 의사결정이 될 수도 있다는 것이다.
결정론적 방법론의 접근은 실제 결과값이 가질 수 있는 값의 변화 범위를 알수 없고 우리가 손실을 볼수 있는 가능성 그리고 우리가 기대하는 값의 실현 가능성 등의 확률 정보를 알 수 없다 그렇게 때문에 리스크를 과소평가하는 위험 또는 리스크를 과대 평가하는 위험에 직면할 수 있게 된다.
확률론적 방법이 반드시 정답은 아니지만 보다 현실적으로 리스크를 평가할 수 있는 방법이 아닐까 생각해 본다.
크리스탈볼 소개를 위한 카탈로그 입니다.
#몬테카를로 시뮬레이션 # 크리스탈볼 # 분포 적합 # 최적화
1. 리스크(Risk)란 무엇인가?
리스크와 불확실성은 대부분의 기업과 정부기관에서 관리하고자 하는 중요한 요인이다. 그래서 이것의 원인을 파악하고 이해하려고 할 것이며, 최종적으론 현명한 의사결정을 내리려 한다. 리스크 용어의 의미는 국가와 그 기준에 따라 다양하게 해석될 수가 있다. 여기서 말하는 리스크란 계량화 혹은 정량화 할 수 있는 것을 의미한다.
2. 리스크 분석(Risk Analysis)이란?
현재의 혹은 미래에 발생할 수 있는 사건에 대하여 정량적 평가를 통하여 그 가능성(Probability)을 예측하고 그 결과를 바탕으로 최선의 의사결정을 할 수가 있어야 한다. 즉, 리스크의 발생 가능성을미리 파악할 수만 있다면 위험을 최소화 하면서 성공 확률은 극대화 할 수 있을 것이다.
3. 확률 사건이란?
같은 원인에서 특정한 결과가 나타나는 비율을 확률이라 말한다. 예를 들어, 정육면체인 주사위를 던졌을 때, 특정한 면이 나타나는 확률이 1/6이다. 또한 앞뒤가 대칭인 동전을 던졌을 때 특정한 면이 나타나는 확률은 1/2이다. 이와 같이 원인과 결과의 관계가 겉보기에 명확한 경우에는 경험에 비추어 그 확률이 계산될 수 있다. 이 경우 우리는 주사위나 동전을 실제로 몇 회까지 던지는 시도를 해봄으로써 통계적 확률이 큰 수의 법칙(law of great number)에 의해서 수학적 확률에 근사 하는 것을 알아 냈다. 하지만 우리는 단지 몇 회의 시도만으로 확인할 수 없는 확률 사건은 어떻게 예측할 것인가?
4. 수학자는 도박에 능하다?
모든 수학자들이 그런 것은 아니겠지만 확률을 분석할 줄 아는 능력이 있으면 도박에서 돈을 딸 가능성이 높은 것은 사실이다. 역사적으로 도박을 통해 확률, 통계이론을 체계화하기 시작한 것은 17세기부터이다. 당시 석학으로 꼽히던 파스칼은 도박사 친구인 드미어가 문의한 주사위 문제를 푸는 과정에서 "파스칼의 삼각형"으로 유명한 이항 전개 계수를 발견했다. 그리고 수학자 페르마와 서신교환을 통해 이를 정리했다. 수학자 폰 노이만과 물리학자 페르미는 확률과 통계이론에 쓰이는 반복실험(시뮬레이션)을 이용해 원자폭탄의 중성자 충돌 확률을 계산해 냈다. 원자폭탄 개발로 이어진 이 시뮬레이션은 도박 도시의 이름을 따서 "몬테카를로 방법"이라고 명명했다.
5. 리스크를 정량화하다!
예를 하나 들어보자. 은행에서 고객들이 일렬로 줄을 지어 업무(서비스)를 보려고 기다리고 있다. 우리는 다음과 같은 정보를 알 수가 있다면
- 시간당 고객의 평균 도착시간
- 한 창구에서 시간당 처리할 수 있는 고객의 평균 수
- 고객 대응이 가능한 창구의 수
위의 정보를 근거로 하여 분석자는 수리적 모형을 구현하여 다음과 같은 결과들을 예측할 수 있을 것이다.
- 고객의 평균 대기 시간
- 은행 업무에 걸리는 평균 시간
- 대기 열에서 기다리고 있는 고객의 평균 수
- 고객이 열에서 특정 T 시간 이상 기다릴 확률
우리는 위의 결과를 바탕으로 해당 은행이 몇 개의 창구를 열어야 고객이 불편함을 느끼지 않을지, 그리고 몇 명의 직원이 더 필요할지/줄어야 할지를 결정할 수가 있을 것이다.
6. 몬테카를로 방법을 통하여 리스크의 실체를 파악하자!
점 추정(single point) 혹은 결정론적(deterministic) 모델링 방식은 해당 평균값들에 대한 best guess를 예측한다. 이 best guess 주변에서 발생 가능한 여러 가지 값들의 조합을 만들어 예측하는 방법이 "what if" 시나리오 분석이다.
공사비 결정에 관한 다음의 간단한 예를 살펴보자.
아래 [표1-1]에서와 같이 우리는 5가지의 비용을 고려하여야 한다. 각 해당 값들은 최소, 최빈, 최대값을 가질 수 있다. "what if" 시나리오 분석을 실시한다면 35 = 243가지의 결과를 예측 할 수 있을 것이다
[표1- 1] 공사비 현황
이 모든 경우의 수를 계산하려면 많은 시간이 소요될 것이다. 게다가, 실제 환경에서는 이보다 많은 경우의 수와 그리고 각 해당 값들은 특정한 분포를 가지고 있음을 알 수가 있다. 즉, 굴착 비용은 $33,200의 평균과 $1,500의 표준편차의 가지는 정규 분포, 토대 비용은 삼각분포, 구조물 비용은 일양 분포 즉, 분포로 정의된 각각의 값들을 가지고 "what if" 시나리오 분석 실시한다면, 결코 인간의 능력만을 가지고는 해결 할 수가 없을 것이다. 그리고 현재 우리가 흔히 분석하는 결정론적 방식으로도 불가능 할 것이다.
이 한계성과 문제점을 해결해 줄 수 있는 방법이 몬테카를로 시뮬레이션이다. 즉, "what if" 방식과는 유사지만, 임의의 난수 발생을 통하여 모든 경우의 수를 따져 보고 그 결과(output)의 발생 분포와 통계량을 제공해 줄 것이다. 아래의 [그림1-1]이 몬테카를로 시뮬레이션의 개념을 잘 설명해 주고 있다.
[그림1-1] 몬테카를로 시뮬레이션 개념