

Dramatically Improve the Quality of Your Strategic Business Decisions
Fortini's clutch Assembly 도면에서 Overrunning Clutch는 그림<1>과 같이 3개의 부품, 즉 허브(hub), 롤러베어링(roller bearing) 4개, 케이지(cage)로 구성되어 있다. 롤러베어링과 케이지 접점사이의 접점각(contact angle)을 요구 Gap(틈새)이라고 하면 구하고자 하는 접점각과 4개의 부품사이의 관계식은 다음과 같이 나타낼 수 있다.
<그림 2>는 Creveling(3)이 접점각 Y에 대해 삼각함수로 유도되는 과정을 일반인들이 쉽게 이해할 수 있도록 설명한 그림으로 접점각은 arccos에 의해 구해지는 것을 확인할 수 있다.
본 비선형 사례에서는 각 부품들의 명목치수와 초기 공차가 주어지면 조립공차가 요구 규격에 대해 어떤 성능을 갖는지에 대한 시뮬레이션을 통한 공차분석 만을 수행하였다. 2005년 크리스탈볼 웹진 11, 12월 호에서 허용차 분석과 허용차 할당이란 내용으로 실린 내용을 상기해 보도록 하자. 허용차 분석 과정은 각 부품 공차정보에 따라 조립품의 공차 결과를 확률적으로 파악하는 것이 된다. 지금 소개하는 비선형 사례에서는 비용에 대한 정보가 없는 관계로 최적화 과정이라 할 수 있는 허용차 할당 분석을 생략하기로 하였다. Overrunning Clutch 사례에서 구성 요소인 3가지 부품이 실제 가공공정에서 각 부품의 가공치수가 어떤 분포(산포)를 가지는가에 따라 조립품의 결과는 달라진다. 이전에 동일한 부품이나 유사한 부품을 가공한 가공치수가 있다면, 크리스탈볼은 분포적합 기능을 통해서 적합한 확률 분포를 찾아낼 것이다. 하지만 본 사례에서는 과거 수집된 자료가 없으므로 일반적으로 많이 사용하는 분포를 적용하도록 할 것이다. 흔히 MIN/MAX 법이라고 하는 Worst Case 방법으로 각 부품의 가공치수가 공차의 극단점에서 발생한다는 가정을 가지고 조립품 공차를 구하는 방법이다. 이와 유사한 분포로는 각 부품이 일양분포(Uniform)를 따르는 것으로 가정하는 한 방법이 있고, 두 번째는 현장에서 가장 많이 접하는 정규분포를 가정하는 방법이다. 본 사례에서는 두 방법을 각각 적용하였을 때 조립품의 요구 규격 결과 차트와 공정성능 분석 자료를 통하여 어떻게 차이가 있는지 비교해 볼 것이다.
3. 엑셀 스프레드시트 모델
조립품의 요구 공차{Y=0.122 ± 0.035 rad (7.0 ±2.0 deg)}에 대해 몬테카를로 시뮬레이션을 실시하기 위해 <그림 3>과 같은 엑셀 스프레드시트에 각 부품의 기본정보를 입력하고 조립품 공차 Y에 대해 비선형 함수식을 입력함으로써 엑셀 스프레드시트 모델을 완성한다. 구축된 엑셀 스프레드시트 모델에 각 부품에 대해 분포 정의와 조립품의 함수식에 대해 예측을 정의하는 과정을 살펴보기로 한다.
각 부품의 공차를 나타내는 분포를 정의하는 내용을 잠깐 살펴보면 명목치수를 입력한 Cell D6에서 가정 정의 메뉴를 선택하여 해당 분포를 선택하고 모수를 정의하면 <그림 4>와 같이 확률 분포가 정의 된다.
셀 D6에서 D9까지 입력된 4개 부품에 대해 분포를 정의하고 앞에서 정의한 조립품 공차(Y)를 나타내는 함수식{Y=f(X1,X2,X3,X4)}을 Cell D12에 입력한 후 조립품 공차를 나타내는 예측을 정의하기 위해 Cell C11에 예측 정의 메뉴를 선택한 후 <그림 5>와 같이 정의하면 Angle의 공차에 대한 분포를 생성할 수 있다.
4. 몬테카를로 시뮬레이션 분석
입력 변수들에 대한 확률 분포의 가정과 예측 정의가 끝났다면 시뮬레이션 실행을 위한 옵션을 지정할 수 있는 실행환경설정 메뉴에서 난수 발생횟수(본 사례에서 1,000,000회)와 공정능력지수를 구하는 항목 등을 체크한 후 시뮬레이션을 실행하면 롤러베어링과 케이지 접점사이의 접점각(contact angle)의 두 개의 분포를 얻게 된다.
첫 째 각 부품에 일양분포를 적용한 조립품의 접점각의 확률분포를 살펴보면 요구 규격에 대해 만족하는 확실성이 다소 부족한 결과를 보여주고 있다. 우측 통계량을 살펴보면 장기 Z Benchmark는 2.74로 단기 Z Benchmark는 4.24로 6시그마 제품 설계를 목표로 한다면 각 부품의 공차를 줄여서 조립품의 품질수준을 더욱 높여야 하는 최적화 과정이 필요할 것이다.
둘 째 각 부품에 정규분포를 적용한 조립품의 접점각의 확률분포를 살펴보면 요구 규격에 대해 만족하는 확실성이 많이 높아진 결과를 보여주고 있다. 우측 통계량을 살펴보면 장기 Z Benchmark는 3.91, 단기 Z Benchmark는 5.41로 6시그마 제품 설계를 목표로 한다면 다소 부족한 품질수준을 만족하기 위해서는 각 부품의 공차를 조금씩 줄여야 하는 최적화 과정이 필요할 것이다.
5. 결론
롤러베어링과 케이지 접점사이의 접점각(Y)은 비선형 모형이나 몬테카를로 시뮬레이션을 통하여 접점각의 요구규격(0.087 ~ 0.157 rad)을 만족하는 확률적인 결과를 알 수 있다. 통상 설계실에서 사용하는 Worst Case 방법은 극단점에서 각 부품의 공차가 발생한다는 가정으로 조립품의 공차는 극단적으로 커지게 됩니다. 그렇게 되면 조립품의 요구규격을 만족하려고 부품의 공차를 극단적으로 작게 할당하는 문제가 발생합니다. 크리스탈볼을 사용한 몬테카를로 시뮬레이션에서는 각 부품에 대해 다양한 분포를 적용하여 극단적으로 작은 공차를 피할 수 있으므로 전체 가공비용을 줄일 수 있는 제품 설계가 가능하게 됩니다.
본 사례에서 다소 아쉬운 것은 참고 논문(Greenwood & Chase)에 의사결정 변수라 할 수 있는 비용정보가 알려져 있지 않아서 최적화 과정인 OptQuest를 통한 공차 할당을 실행하지 못한 점입니다. 본 사례의 소개 목적은 비선형 모형에 대해 몬테카를로 시뮬레이션을 적용할 수 있다는 것을 보여줌으로써 산업현장에 널리 사용되고 있는 비선형 모형에 대해서 크리스탈볼 툴에 의한 확률론적인 공차 분석을 적극 활용했으면 하는 소망으로 소개를 마치고자 합니다.
참고문헌
1. Fortini, E. I., Dimensioning for Interchangeable Manufacturing, Industrial Press, New York, 1967, p.48
2. Greenwood, W. H., Chase, K. W., "Worst Case Analysis with Nonlinear Problem", ASME Jounal of Engineering for Industry, Vol. 110, Aug, 88, pp. 232-235
3. Creveling, C. M., Tolerace Design : A Hand book for Developing Optimal Specification, Addison-Welsey (1997)
여러분은 어떤 프로젝트를 완료하는데 다음과 같이 7단계를 거쳐야 한다는 것을 파악하였다.
대략적으로 소요되는 일정은 [표1-1]와 같으며, 우리가 프로젝트를 계획한 일정 내에 마칠 가능성에 대해서 예측을 해보겠다
[표1- 1] 프로젝트 각 단계별 소요 시간
(참고) 가중평균 : (a+4b+c) / 6, 분산 : [(c-a) / 6]2,, 표준편차 : [(c-a) / 6]
작업 진행 경로는 다음 [그림1-2]와 같으며, 두 가지 경로가 존재하고 있다.
[그림1- 2] 프로젝트 진행 경로
우리는 아주 기본적인 방법으로 통하여 다음과 같이 작업 소요 시간을 예측해 볼 수가 있을 것이다.
[표1-2] 프로젝트 완료 시간
위의 스케줄 표만으로도 좋은 정보를 얻을 수 있지만 이미 우리는 몬테카를로 시뮬레이션 기법을 배웠기 때문에 좀더 정확한 분석을 시도해 보겠다.
크리스탈볼을 활용하여 시뮬레이션을 수행하기 위해서 아래의 단계를 고려하여 분석을 하면 될 것이다.
- 각 단계에서 발생하는 소요 시간을 파악한다.
- 작업의 진행 단계 및 소요 기간을 엑셀에 정의한다.
- Crystal Ball 기능을 이용하여 분포를 정의하고 시뮬레이션을 실시한다.
여기의 분포는 낙관적 0.1%, 평균 50% 그리고 비관적 99.9%의 베타 분포로 정의한다.
- 결과로서 실제 예상되는 기간의 분포와 통계량을 확인한다.
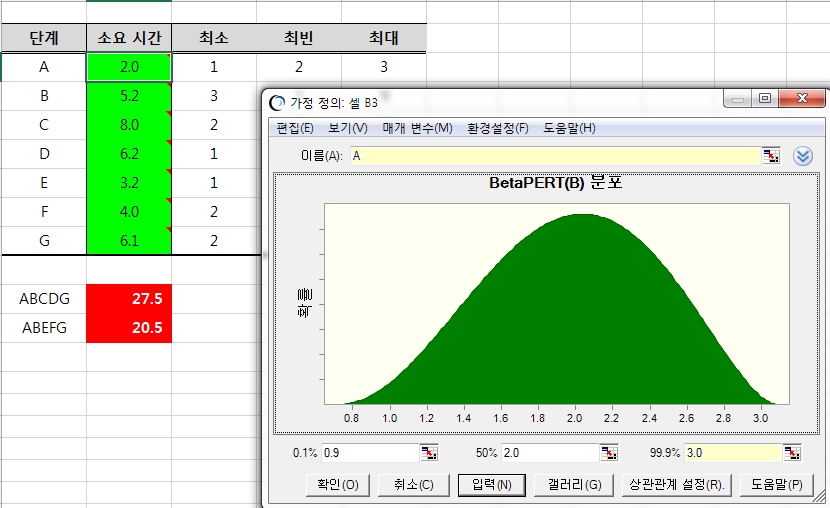
[그림 1-1] 크리스탈볼 모델링
위의 [그림 1-1]과 같이 엑셀에 시뮬레이션 모델일을 구현한 후 실행하면 그림 [1-2]와 같은 결과를 얻을 수 있다.
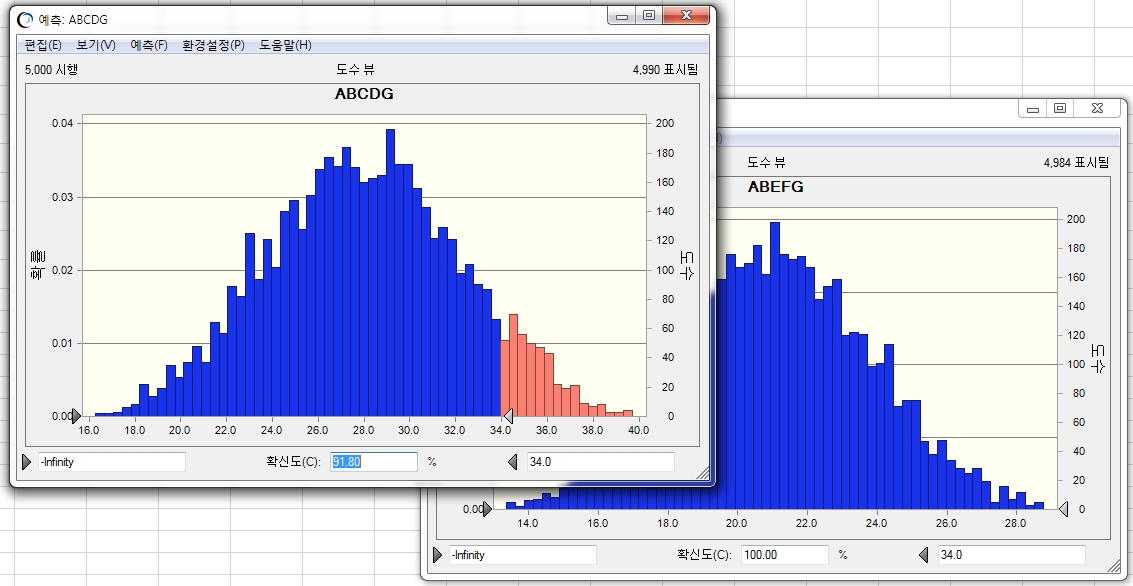
[그림 1-2] 프로젝트 경로별 시뮬레이션 결과
[그림 1-2]는 프로젝트의 2가지 경로에 대한 시뮬레이션 결과를 제공하고 있다.
우리가 이 프로젝트를 34주만에 마치기를 원할 경우 각각의 경로에 대한 프로젝트 기간을 예측해 보면 ABCDG는 91.8%, ABEFG는 100%임을 알 수가 있다.
따라서 ABCDG가 프로젝트의 CPM임을 파악할 수 있으며 프로젝트를 34주 이내에 끝마치기 위해서 이 경로에 대한 관리가 더 철저히 이루어 져야 한다는 것을 알 수 있다.
기존에 우리가 평균적으로 예측한 27주는 너무 리스크가 큰 일정이므로 조정이 필요함을 알 수 있다.
우리는 시뮬레이션을 통하여 보다 현실적이며 지연이라는 리스크를 고려한 프로젝트 일정에 대해 예측해 볼 수 있다.